RLlib を使ってナップサック問題を強化学習
ナップサック問題へ強化学習を適用すると、どうなるのか気になったので試してみました。
強化学習には、Ray に含まれている RLlib を使い、Jupyter Notebook 上で実行します。
今回のサンプルコードは http://github.com/fits/try_samples/tree/master/blog/20200922/
はじめに
以下のようにして Ray と RLlib をインストールしておきます。(TensorFlow も事前にインストールしておく)
Ray インストール
> pip install ray[rllib]
ナップサック問題
今回は、以下のような価値と重さを持った品物に対して、重さの合計が 35 以下で価値の合計を最大化する品物の組み合わせを探索する事にします。
| 価値 | 重さ |
|---|---|
| 105 | 10 |
| 74 | 7 |
| 164 | 15 |
| 32 | 3 |
| 235 | 22 |
品物をそれぞれ 1個までしか選べない場合(0-1 ナップサック問題)の最適な組み合わせは、以下のように 5番目以外を 1個ずつ選ぶ事です。(価値の合計は 375)
価値 375 の組み合わせ(0-1 ナップサック問題の最適解)
1, 1, 1, 1, 0
また、同じ品物をいくらでも選べる場合の最適な組み合わせは以下のようになります。(価値の合計は 376)
価値 376 の組み合わせ
0, 2, 1, 2, 0
強化学習でこのような組み合わせを導き出す事ができるのか確認します。
1. サンプル1 - sample1.ipynb
とりあえず、強化学習における状態・行動・報酬を以下のようにしてみました。 エピソードは、指定した回数(今回は 10回)の行動を行う事で終了とします。
| 状態 | 行動 | (即時)報酬 |
|---|---|---|
| 品物毎の個数 | 品物の個数を操作(-1, +1) | 価値の合計 |
行動は以下のような 0 ~ 10 の数値で表現する事にします。
- 0 = 1番目の品物の個数を -1
- 1 = 1番目の品物の個数を +1
- ・・・
- 8 = 5番目の品物の個数を -1
- 9 = 5番目の品物の個数を +1
- 10 = 個数を変更しない(現状維持)
これらを OpenAI Gym で定義したのが次のコードです。
環境は gym.Env を継承し、__init__ で行動空間(action_space)と状態空間(observation_space)を定義、reset で状態の初期化、step で状態の更新と報酬の算出を行うように実装します。
step の戻り値は、更新後の状態、報酬、エピソード終了か否か、(デバッグ用途等の)情報 となっています。
Discrete(n) は 0 ~ n - 1 の整数値、Box は low ~ high の実数値の多次元配列となっており、、行動空間と状態空間の定義にそれぞれ使用しています。
環境定義
import gym from gym.spaces import Discrete, Box def next_state(items, state, action): idx = action // 2 act = action % 2 if idx < len(items): state[idx] += (1 if act == 1 else -1) return state # 報酬の算出 def calc_reward(items, state, max_weight, burst_reward): reward = 0 weight = 0 for i in range(len(state)): reward += items[i][0] * state[i] weight += items[i][1] * state[i] if weight > max_weight or min(state) < 0: reward = burst_reward return reward, weight class Knapsack(gym.Env): def __init__(self, config): self.items = config["items"] # 重さの上限値 self.max_weight = config["max_weight"] # 行動の回数 self.max_count = config["max_count"] # 重さが超過するか、個数が負の数となった場合の報酬 self.burst_reward = config["burst_reward"] n = self.max_count # 行動空間の定義 self.action_space = Discrete(len(self.items) * 2 + 1) # 状態空間の定義 self.observation_space = Box(low = -n, high = n, shape = (len(self.items), )) self.reset() def reset(self): self.count = 0 self.state = [0 for _ in self.items] return self.state def step(self, action): # 状態の更新 self.state = next_state(self.items, self.state, action) # 報酬の算出 reward, _ = calc_reward(self.items, self.state, self.max_weight, self.burst_reward) self.count += 1 # エピソード完了の判定 done = self.count >= self.max_count return self.state, reward, done, {}
次に上記環境のための設定を行います。
env_config の内容が __init__ の config 引数となります。
重さの上限値を超えた場合や個数が負の数となった場合の報酬(burst_reward)をとりあえず -100 としています。
なお、基本的に RLlib のデフォルト設定値を使う事にします。
設定
items = [
[105, 10],
[74, 7],
[164, 15],
[32, 3],
[235, 22]
]
config = {
"env": Knapsack,
"env_config": {"items": items, "max_count": 10, "max_weight": 35, "burst_reward": -100}
}
強化学習を実施する前に、Ray を初期化しておきます。
Ray 初期化
import ray
ray.init()
(a) PPO(Proximal Policy Optimization)
PPO アルゴリズムを試してみます。
トレーナーの定義 - PPO
from ray.rllib.agents.ppo import PPOTrainer trainer = PPOTrainer(config = config)
まずは、学習(train の実行)を 10回繰り返してみます。
後で学習時の状況を確認するために episode_reward_max 等の値を保持するようにしています。
学習
r_max = [] r_min = [] r_mean = []
from ray.tune.logger import pretty_print for _ in range(10): r = trainer.train() print(pretty_print(r)) r_max.append(r["episode_reward_max"]) # 最大 r_min.append(r["episode_reward_min"]) # 最小 r_mean.append(r["episode_reward_mean"]) # 平均
以下のコードで結果を確認してみます。
compute_action を呼び出す事で、指定した状態に対する行動を取得できます。
評価1
s = [0 for _ in range(len(items))] for _ in range(config["env_config"]["max_count"]): a = trainer.compute_action(s) s = next_state(items, s, a) r, w = calc_reward(items, s, config["env_config"]["max_weight"], config["env_config"]["burst_reward"]) print(f"{a}, {s}, {r}, {w}")
下記のように、価値の合計が 375 となる組み合わせ(0-1 ナップサック問題とした場合の最適解)が現れており、ある程度は学習できているように見えます。
評価1の結果 - PPO 学習 10回
1, [1, 0, 0, 0, 0], 105, 10 3, [1, 1, 0, 0, 0], 179, 17 5, [1, 1, 1, 0, 0], 343, 32 7, [1, 1, 1, 1, 0], 375, 35 7, [1, 1, 1, 2, 0], -100, 38 6, [1, 1, 1, 1, 0], 375, 35 0, [0, 1, 1, 1, 0], 270, 25 1, [1, 1, 1, 1, 0], 375, 35 6, [1, 1, 1, 0, 0], 343, 32 7, [1, 1, 1, 1, 0], 375, 35
これだけだとよく分からないので、100回繰り返してそれぞれの報酬の最高値をカウントしてみます。
評価2
import collections rs = [] for _ in range(100): s = [0 for _ in range(len(items))] r_tmp = config["env_config"]["burst_reward"] for _ in range(config["env_config"]["max_count"]): a = trainer.compute_action(s) s = next_state(items, s, a) r, w = calc_reward(items, s, config["env_config"]["max_weight"], config["env_config"]["burst_reward"]) r_tmp = max(r, r_tmp) rs.append(r_tmp) collections.Counter(rs)
結果は以下のようになりました。 最高値の 376 ではなく 375 の組み合わせへ向かうように学習が進んでいるように見えます。
評価2の結果 - PPO 学習 10回
Counter({302: 6,
309: 2,
284: 1,
343: 12,
375: 39,
270: 4,
341: 7,
373: 1,
340: 2,
269: 1,
372: 6,
301: 4,
376: 1,
334: 2,
333: 2,
344: 1,
299: 4,
317: 1,
275: 1,
349: 1,
316: 1,
312: 1})
更に、学習を 10回繰り返した後の結果です。 375 へ向かって収束しているように見えます。
評価1の結果 - PPO 学習 20回
1, [1, 0, 0, 0, 0], 105, 10 5, [1, 0, 1, 0, 0], 269, 25 3, [1, 1, 1, 0, 0], 343, 32 7, [1, 1, 1, 1, 0], 375, 35 10, [1, 1, 1, 1, 0], 375, 35 10, [1, 1, 1, 1, 0], 375, 35 10, [1, 1, 1, 1, 0], 375, 35 2, [1, 0, 1, 1, 0], 301, 28 3, [1, 1, 1, 1, 0], 375, 35 0, [0, 1, 1, 1, 0], 270, 25
評価2の結果 - PPO 学習 20回
Counter({375: 69, 373: 18, 376: 3, 341: 5, 372: 1, 302: 1, 344: 3})
50回学習した後の結果は以下のようになりました。
評価2の結果 - PPO 学習 50回
Counter({375: 98, 373: 2})
ここまでの(学習時の)報酬状況をグラフ化してみます。
学習回数と報酬のグラフ化
%matplotlib inline import matplotlib.pyplot as plt plt.plot(r_max, label = "reward_max", color = "red") plt.plot(r_min, label = "reward_min", color = "green") plt.plot(r_mean, label = "reward_mean", color = "blue") plt.legend(loc = "upper left") plt.ylim([-1000, 3700]) plt.ylabel("reward") plt.show()
学習時の報酬グラフ - PPO 学習 50回
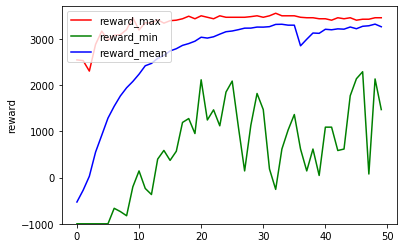
エピソード内の報酬を高めていくには重量超過やマイナス個数を避けるのが重要、それには各品物の個数を 0 か 1 にしておくのが無難なため、0-1 ナップサック問題としての最適解へ向かっていくのかもしれません。
(b) DQN(Deep Q-Network)
比較のために DQN でも実行してみます。
PPOTrainer の代わりに DQNTrainer を使うだけです。
トレーナーの定義 - DQN
from ray.rllib.agents.dqn import DQNTrainer trainer = DQNTrainer(config = config)
10回の学習では以下のような結果となりました。
評価1の結果 - DQN 学習 10回
5, [0, 0, 1, 0, 0], 164, 15 7, [0, 0, 1, 1, 0], 196, 18 2, [0, -1, 1, 1, 0], -100, 11 5, [0, -1, 2, 1, 0], -100, 26 2, [0, -2, 2, 1, 0], -100, 19 0, [-1, -2, 2, 1, 0], -100, 9 1, [0, -2, 2, 1, 0], -100, 19 3, [0, -1, 2, 1, 0], -100, 26 5, [0, -1, 3, 1, 0], -100, 41 6, [0, -1, 3, 0, 0], -100, 38
評価2の結果 - DQN 学習 10回
Counter({-100: 33,
360: 1,
105: 8,
270: 2,
372: 5,
315: 1,
0: 5,
374: 1,
74: 2,
274: 1,
235: 7,
340: 3,
32: 4,
164: 5,
238: 1,
309: 2,
106: 1,
228: 2,
169: 1,
267: 3,
343: 1,
196: 1,
331: 1,
363: 1,
254: 1,
299: 1,
317: 1,
212: 1,
301: 1,
328: 1,
138: 1,
64: 1})
DQN は PPO に比べて episodes_total(学習で実施したエピソード数の合計)が 1/4 程度と少なかったので、40回まで実施してみました。
評価1の結果 - DQN 学習 40回
6, [0, 0, 0, -1, 0], -100, -3 7, [0, 0, 0, 0, 0], 0, 0 1, [1, 0, 0, 0, 0], 105, 10 4, [1, 0, -1, 0, 0], -100, -5 4, [1, 0, -2, 0, 0], -100, -20 8, [1, 0, -2, 0, -1], -100, -42 7, [1, 0, -2, 1, -1], -100, -39 1, [2, 0, -2, 1, -1], -100, -29 2, [2, -1, -2, 1, -1], -100, -36 4, [2, -1, -3, 1, -1], -100, -51
評価2の結果 - DQN 学習 40回
Counter({0: 5,
328: 4,
164: 8,
-100: 28,
340: 5,
228: 1,
309: 4,
74: 1,
238: 4,
235: 7,
32: 3,
358: 2,
343: 2,
196: 2,
269: 3,
372: 2,
365: 1,
179: 2,
374: 1,
302: 1,
106: 3,
312: 1,
105: 5,
270: 2,
148: 2,
360: 1})
80回学習した結果です。
評価1 - DQN 学習 80回
5, [0, 0, 1, 0, 0], 164, 15 1, [1, 0, 1, 0, 0], 269, 25 7, [1, 0, 1, 1, 0], 301, 28 4, [1, 0, 0, 1, 0], 137, 13 0, [0, 0, 0, 1, 0], 32, 3 2, [0, -1, 0, 1, 0], -100, -4 7, [0, -1, 0, 2, 0], -100, -1 1, [1, -1, 0, 2, 0], -100, 9 0, [0, -1, 0, 2, 0], -100, -1 4, [0, -1, -1, 2, 0], -100, -16
評価2 - DQN 学習 80回
Counter({-100: 5,
269: 8,
164: 20,
301: 3,
211: 2,
235: 7,
105: 3,
372: 2,
333: 1,
238: 2,
316: 2,
196: 2,
253: 1,
242: 2,
312: 3,
343: 3,
340: 9,
179: 2,
267: 3,
270: 1,
74: 3,
328: 9,
309: 2,
284: 1,
137: 1,
285: 1,
360: 1,
374: 1})
200回学習した結果です。
評価2 - DQN 学習 200回
Counter({-100: 8,
238: 4,
340: 10,
0: 4,
267: 6,
106: 1,
74: 7,
105: 1,
328: 4,
235: 33,
309: 9,
228: 1,
270: 2,
32: 1,
301: 1,
196: 3,
341: 2,
269: 1,
374: 1,
372: 1})
学習時の報酬グラフは以下の通り、PPO のようにスムーズに学習が進んでおらず、DQN は本件に向いていないのかもしれません。
学習時の報酬グラフ - DQN 学習 200回

これは、報酬のクリッピング ※ に因るものかとも思いましたが、RLlib における報酬クリッピングの設定 clip_rewards はデフォルトで None であり、DQN のデフォルト設定 (dqn.py の DEFAULT_CONFIG) においても有効化しているような箇所は見当たりませんでした。
他の箇所で実施しているのかもしれませんが、今回は確認できませんでした。
※ 基本的には、 元の報酬の符号に合わせて 1, -1, 0 のいずれかに報酬の値が変更されてしまい、 報酬の大小は考慮されなくなる 本件であれば、 重量超過やマイナス個数のように報酬がマイナスにならない行動であれば どれでも良い事になってしまうと思われる
ちなみに、clip_rewards を True に設定した PPOTrainer を使ってみたところ、結果が著しく悪化しました。(マイナス報酬を避けるだけになった)
2. サンプル2 - sample2.ipynb
次に、行動によってのみ次の状態を決定するようにしてみます。 エピソードは 1回の行動で終了とします。
| 状態 | 行動 | (即時)報酬 |
|---|---|---|
| 品物毎の個数 | 品物毎の個数 | 価値の合計 |
この場合、action_space も Box で定義する事になります。
最軽量の品物が重要制限内で選択できる最大の個数を Box の最大値としています。
環境定義
def next_state(action): return [round(d) for d in action] def calc_reward(items, state, max_weight, burst_reward): reward = 0 weight = 0 for i in range(len(state)): reward += items[i][0] * state[i] weight += items[i][1] * state[i] if weight > max_weight or min(state) < 0: reward = burst_reward return reward, weight class Knapsack(gym.Env): def __init__(self, config): self.items = config["items"] self.max_weight = config["max_weight"] self.burst_reward = config["burst_reward"] # 個数の最大値 n = self.max_weight // min(np.array(self.items)[:, 1]) self.action_space = Box(0, n, shape = (len(self.items), )) self.observation_space = Box(0, n, shape = (len(self.items), )) def reset(self): return [0 for _ in self.items] def step(self, action): state = next_state(action) reward, _ = calc_reward(self.items, state, self.max_weight, self.burst_reward) return state, reward, True, {}
設定
items = [
[105, 10],
[74, 7],
[164, 15],
[32, 3],
[235, 22]
]
config = {
"env": Knapsack,
"env_config": {"items": items, "max_weight": 35, "burst_reward": -100}
}
(a) PPO(Proximal Policy Optimization)
PPO で実施してみます。
基本的な処理内容は 1. サンプル1 と同じですが、行動 1回でエピソードが終了するため、以下のコードで結果を確認する事にします。
評価
import collections rs = [] for _ in range(100): s = [0 for _ in range(len(items))] a = trainer.compute_action(s) s = next_state(a) r, _ = calc_reward(items, s, config["env_config"]["max_weight"], config["env_config"]["burst_reward"]) rs.append(r) collections.Counter(rs)
70回学習後の結果です。
評価結果 - PPO 学習 70回
Counter({375.0: 100})
学習時の状況は以下のようになりました。
学習時の報酬グラフ - PPO 学習 70回

(b) DDPG(Deep Deterministic Policy Gradient)
action_space が Box の場合に、DQNTrainer が UnsupportedSpaceException エラーを発生させるので、DQN は使えませんでした。
そこで、DDPG を使ってみました。
トレーナーの定義 - DDPG
from ray.rllib.agents.ddpg import DDPGTrainer trainer = DDPGTrainer(config = config)
こちらは、PPO 等と比べて処理に時間がかかる上に、80回学習しても順調とはいえない結果となりました。
学習時の報酬グラフ - DDPG 学習 80回

評価結果 - DDPG 学習 80回
Counter({347.0: 18, -100: 79, 242.0: 3})
以下のように評価の回数を 1000 にして再度確認してみます。
for _ in range(1000): s = [0 for _ in range(len(items))] a = trainer.compute_action(s) ・・・ collections.Counter(rs)
評価結果(1000回) - DDPG 学習 80回
Counter({347.0: 232,
-100: 718,
242.0: 24,
315.0: 14,
210.0: 1,
316.0: 7,
274.0: 3,
374.0: 1})
347(3, 0, 0, 1, 0)が多くなっているのはよく分かりませんが、DDPG も本件に向いていないのかもしれません。