トピックモデルは潜在的なトピックから文書中の単語が生成されると仮定するモデルのようです。

であれば、これを「Python でアソシエーション分析」で行ったような併売の分析に適用するとどうなるのか気になったので、gensim の LdaModel を使って同様のデータセットを LDA（潜在的ディリクレ配分法）で処理してみました。

ソースは http://github.com/fits/try_samples/tree/master/blog/20180313/

1. はじめに

データセット

gensim で LDA を処理する場合、通常は以下のような lowcorpus フォーマットを使った方が簡単なようです。（LowCorpus で処理できるので）

<文書数>
<文書1の単語1> <文書1の単語2> ・・・
<文書2の単語1> <文書2の単語2> ・・・
・・・

ただ、1行目が冗長なように思うので、今回は word2vec 等でも使えるように 1行目を除いたデータファイルを使います。

内容としては「Python でアソシエーション分析」の data.basket ファイルをスペース区切りにしただけです。

data.txt

C S M R
T Y C
P Y C M
O W L
R
O U R L
P
W C
T O W B C
C T W B Y F D
・・・
R P S
B
B S
B F
C F N

2. LDA の適用

(1) 辞書とコーパスの作成

まずは、ファイルを読み込んで辞書 Dictionary とコーパスを作成します。

単語部分が文字列のままでは処理できないため、単語を一意の ID（数値）へマッピングする Dictionary を用意し、doc2bow で文書を [(<単語ID>, <出現数>), ・・・] のような形式 bag-of-words へ変換しコーパスを作ります。

word2vec.LineSentence を用いてデータファイルを読み込み、併売の分析という点から単一要素の行を除外してみました。

from gensim.corpora import Dictionary
from gensim.models import word2vec

# 単一要素の行は除外
sentences = [s for s in word2vec.LineSentence('data.txt') if len(s) >= 2]

dic = Dictionary(sentences)

corpus = [dic.doc2bow(s) for s in sentences]

変数の内容はそれぞれ以下のようになります。

sentences の内容

[['C', 'S', 'M', 'R'],
 ['T', 'Y', 'C'],
 ['P', 'Y', 'C', 'M'],
 ・・・]

dic の内容

{0: 'C',
 1: 'M',
 2: 'R',
 3: 'S',
 ・・・
 16: 'A',
 17: 'G',
 18: 'Z'}

corpus の内容

[[(0, 1), (1, 1), (2, 1), (3, 1)],
 [(0, 1), (4, 1), (5, 1)],
 [(0, 1), (1, 1), (5, 1), (6, 1)],
 ・・・]

(2) LdaModel 作成

LdaModel は (1) の辞書とコーパスを使って作成できます。 id2word は必須ではありませんが、使用するメソッド次第で必要になるようです。

random_state を指定しない場合、ランダムな値が適用され実行の度に結果が異なります。

from gensim.models.ldamodel import LdaModel

lda = LdaModel(corpus = corpus, id2word = dic, num_topics = 8, alpha = 0.01, random_state = 1)

num_topics と alpha

ここで、トピック数 num_topics と alpha の値が重要となります。

トピックが多すぎると、どの文書にも該当しない（該当する確率が非常に低い）無駄なトピックが作られてしまいますし、逆に少なすぎるとあまり特徴の無いトピックが出来て有用な結果が得られないかもしれません。

alpha はデフォルトで 1 / num_topics の値を適用するようになっていますが、alpha の値によって文書あたりの該当トピック数が大きく変化するため注意が必要です。（大きいとトピック数が増えます）

それでは、alpha の値による影響を確認してみます。

LdaModelオブジェクト[bow] か get_document_topics(bow) を用いると、文書（bag-of-words）に対して確率が 0.01 （デフォルト値）以上のトピックを取得でき、内容は [(トピックID, 値), (トピックID, 値), ・・・] となっています。

from statistics import mean

for t in range(4, 21, 4):
    for n in range(1, 10, 2):
        a = n / 100

        lda = LdaModel(corpus = corpus, id2word = dic, num_topics = t, alpha = a, random_state = 1)

        # 文書の平均トピック数を算出
        r = mean([len(lda[c]) for c in corpus])

        print(f"num_topics = {t}, alpha = {a}, mean = {r}")

結果は以下のようになりました。

併売の分析として考えると、併売されやすいものは同じトピックに集まって欲しいので、平均トピック数の少ない方が望ましいと考えられます。

以下の中では num_topics = 8, alpha = 0.01 が良さそうですので、以後はこの値を使って処理する事にします。

num_topics, alpha と文書あたりの平均トピック数

num_topics = 4, alpha = 0.01, mean = 1.0675675675675675
num_topics = 4, alpha = 0.03, mean = 1.9054054054054055
num_topics = 4, alpha = 0.05, mean = 3.3378378378378377
num_topics = 4, alpha = 0.07, mean = 3.8378378378378377
num_topics = 4, alpha = 0.09, mean = 3.9594594594594597
num_topics = 8, alpha = 0.01, mean = 1.0405405405405406
num_topics = 8, alpha = 0.03, mean = 3.0405405405405403
num_topics = 8, alpha = 0.05, mean = 6.418918918918919
num_topics = 8, alpha = 0.07, mean = 7.648648648648648
num_topics = 8, alpha = 0.09, mean = 7.905405405405405
num_topics = 12, alpha = 0.01, mean = 1.054054054054054
num_topics = 12, alpha = 0.03, mean = 4.202702702702703
num_topics = 12, alpha = 0.05, mean = 9.486486486486486
num_topics = 12, alpha = 0.07, mean = 11.41891891891892
num_topics = 12, alpha = 0.09, mean = 11.85135135135135
num_topics = 16, alpha = 0.01, mean = 1.1081081081081081
num_topics = 16, alpha = 0.03, mean = 5.351351351351352
num_topics = 16, alpha = 0.05, mean = 12.594594594594595
num_topics = 16, alpha = 0.07, mean = 14.432432432432432
num_topics = 16, alpha = 0.09, mean = 15.81081081081081
num_topics = 20, alpha = 0.01, mean = 1.1081081081081081
num_topics = 20, alpha = 0.03, mean = 6.527027027027027
num_topics = 20, alpha = 0.05, mean = 13.297297297297296
num_topics = 20, alpha = 0.07, mean = 17.972972972972972
num_topics = 20, alpha = 0.09, mean = 19.743243243243242

ちなみに、トピック数 20 で処理すると、どの文書にも（0.01 以上で）該当しないトピックが 4個程度発生しました。そのため、このデータセットでは 16 程度がトピック数の最大値だと思われます。

また、参考のために主成分分析（PCA）で処理してみると、次元数 8 の場合に寄与率の累計が 0.76、16 の場合に 0.98 となりました。

coherence と perplexity

一般的なトピックモデルの評価指標としては coherence （トピック性能）と perplexity （予測性能）というものがあるようです。

通常、perplexity は学習用と評価用にデータを分けて算出するようですが、とりあえず今回はデータを分けずに算出してみました。

coherence の算出方法として u_mass 以外にも c_v や c_uci 等が用意されていましたが、LdaModel の top_topics メソッドのデフォルトが u_mass を使っていたのでこれに倣いました。

ソース ldamodel.py を見たところ、log_perplexity の戻り値は単語あたりの bound （perwordbound）となっており、perplexity は 2 の -perwordbound 乗 で算出するようでした。

import numpy as np
from gensim.models.ldamodel import CoherenceModel

for i in range(1, 31):
    lda = LdaModel(corpus = corpus, id2word = dic, num_topics = i, alpha = 0.01, random_state = 1)

    cm = CoherenceModel(model = lda, corpus = corpus, coherence = 'u_mass')
    coherence = cm.get_coherence()

    perwordbound = lda.log_perplexity(corpus)
    perplexity = np.exp2(-perwordbound)

    print(f"num_topics = {i}, coherence = {coherence}, perplexity = {perplexity}")

結果は以下の通りです。

coherence は大きい方が望ましく perplexity は小さい方が望ましいのだと思うのですが、単純にトピック数の大小に影響されているこの結果を見る限りは、今回の用途には適していないように思います。（もしくは、算出方法に誤りがあるのかも）

coherence と perplexity 結果

topic_num = 1, coherence = -10.640923461890344, perplexity = 6.681504324473536
topic_num = 2, coherence = -10.564527218339581, perplexity = 7.59037413046145
topic_num = 3, coherence = -10.51994121341506, perplexity = 8.421586281561325
topic_num = 4, coherence = -10.498935784230891, perplexity = 9.163865911812838
topic_num = 5, coherence = -10.466505553089613, perplexity = 10.02873590975954
topic_num = 6, coherence = -10.427246025202495, perplexity = 10.706792157460887
topic_num = 7, coherence = -10.441670962642908, perplexity = 11.007513545383127
topic_num = 8, coherence = -10.431903836350067, perplexity = 11.393319548027026
topic_num = 9, coherence = -10.394974053783624, perplexity = 13.154796351781842
topic_num = 10, coherence = -10.398193229861565, perplexity = 13.453254319022557
topic_num = 11, coherence = -10.393056192535115, perplexity = 13.771475137747052
topic_num = 12, coherence = -10.386759634629335, perplexity = 14.178980599173155
topic_num = 13, coherence = -10.395241748738718, perplexity = 16.132824693572804
・・・
num_topics = 18, coherence = -10.373039938078676, perplexity = 21.76790238689796
num_topics = 19, coherence = -10.336482759968458, perplexity = 20.067649661316306
topic_num = 20, coherence = -10.318518756029693, perplexity = 21.38207737535069
・・・
num_topics = 28, coherence = -10.297976846891006, perplexity = 25.2833756062596
num_topics = 29, coherence = -10.279231366719717, perplexity = 26.40726049105775
num_topics = 30, coherence = -10.266658546693755, perplexity = 26.52593230907953

(3) 結果の出力

show_topics

show_topics もしくは print_topics でトピックの内容をログ出力します。

ログ出力を有効化していなくても、ログへの出力内容をメソッドの戻り値として取得できます。

topic_num = 8
alpha = 0.01

lda = LdaModel(corpus = corpus, id2word = dic, num_topics = topic_num, alpha = alpha, random_state = 1)

for t in lda.show_topics():
    print(t)

出力結果

(0, '0.259*"C" + 0.131*"T" + 0.100*"N" + 0.068*"O" + 0.068*"F" + 0.068*"P" + 0.068*"B" + 0.036*"D" + 0.036*"W" + 0.036*"R"')
(1, '0.234*"B" + 0.159*"D" + 0.084*"O" + 0.084*"W" + 0.084*"G" + 0.084*"C" + 0.084*"R" + 0.084*"S" + 0.009*"H" + 0.009*"F"')
(2, '0.223*"C" + 0.149*"S" + 0.094*"R" + 0.076*"B" + 0.076*"F" + 0.076*"P" + 0.076*"D" + 0.057*"N" + 0.057*"W" + 0.039*"L"')
(3, '0.172*"S" + 0.172*"N" + 0.172*"C" + 0.172*"R" + 0.091*"Y" + 0.091*"B" + 0.010*"F" + 0.010*"G" + 0.010*"A" + 0.010*"H"')
(4, '0.223*"B" + 0.113*"R" + 0.094*"S" + 0.094*"P" + 0.076*"W" + 0.076*"D" + 0.076*"Y" + 0.057*"C" + 0.057*"M" + 0.039*"T"')
(5, '0.191*"S" + 0.173*"B" + 0.139*"M" + 0.105*"C" + 0.088*"F" + 0.088*"W" + 0.071*"N" + 0.036*"D" + 0.036*"R" + 0.019*"T"')
(6, '0.195*"O" + 0.163*"S" + 0.100*"R" + 0.100*"W" + 0.068*"P" + 0.068*"L" + 0.068*"B" + 0.036*"Y" + 0.036*"U" + 0.036*"T"')
(7, '0.241*"W" + 0.163*"O" + 0.163*"B" + 0.084*"H" + 0.084*"C" + 0.044*"T" + 0.044*"N" + 0.044*"G" + 0.044*"R" + 0.044*"U"')

get_topic_terms

上記は加工された文字列でしたが、get_topic_terms でトピック内の単語とその確率を取得できます。

topn （デフォルトは 10）でトピック内の単語を確率の高い順にいくつ取得するかを指定できます。

from toolz import frequencies

# 文書毎の該当トピック
doc_topics = [lda[c] for c in corpus]
# トピックの該当数
topic_freq = frequencies([t[0] for dt in doc_topics for t in dt])

for i in range(topic_num):
  items = [(dic[t[0]], t[1]) for t in lda.get_topic_terms(i, topn = 5)]

  print(f"topic_id = {i}, freq = {topic_freq[i]}, items = {items}")

出力結果

topic_id = 0, freq = 10, items = [('C', 0.25896409), ('T', 0.13147409), ('N', 0.099601582), ('P', 0.067729078), ('F', 0.067729078)]
topic_id = 1, freq = 4, items = [('B', 0.23364486), ('D', 0.15887851), ('O', 0.084112152), ('W', 0.084112152), ('G', 0.084112152)]
topic_id = 2, freq = 11, items = [('C', 0.22298852), ('S', 0.14942528), ('R', 0.094252877), ('P', 0.075862072), ('B', 0.075862072)]
topic_id = 3, freq = 5, items = [('S', 0.17171718), ('N', 0.17171718), ('C', 0.17171715), ('R', 0.17171715), ('Y', 0.090909086)]
topic_id = 4, freq = 14, items = [('B', 0.22298847), ('R', 0.11264367), ('S', 0.094252862), ('P', 0.094252862), ('W', 0.075862065)]
topic_id = 5, freq = 17, items = [('S', 0.19057818), ('B', 0.17344755), ('M', 0.13918629), ('C', 0.10492505), ('F', 0.087794438)]
topic_id = 6, freq = 8, items = [('O', 0.1952191), ('S', 0.16334662), ('W', 0.099601582), ('R', 0.099601582), ('P', 0.067729086)]
topic_id = 7, freq = 8, items = [('W', 0.24137934), ('O', 0.1625616), ('B', 0.1625616), ('H', 0.083743848), ('C', 0.083743848)]

get_document_topics

上記ではトピックの構成を取得しましたが、get_document_topics で per_word_topics = True を指定すると、文書内の単語がどのトピックへどの程度の確率で該当するかを取得できます。

for i in range(len(corpus)):
  dts = lda.get_document_topics(corpus[i], per_word_topics = True)

  for dt in dts[2]:
    item = dic[dt[0]]
    print(f"corpus = {i}, item = {item}, topic_id = {dt[1]}")

出力結果

corpus = 0, item = C, topic_id = [(5, 1.0000001)]
corpus = 0, item = M, topic_id = [(5, 1.0)]
corpus = 0, item = R, topic_id = [(5, 1.0000001)]
corpus = 0, item = S, topic_id = [(5, 0.99999994)]
corpus = 1, item = C, topic_id = [(0, 1.0000001)]
corpus = 1, item = T, topic_id = [(0, 1.0)]
corpus = 1, item = Y, topic_id = [(0, 1.0)]
corpus = 2, item = C, topic_id = [(4, 1.0)]
corpus = 2, item = M, topic_id = [(4, 1.0)]
corpus = 2, item = Y, topic_id = [(4, 1.0)]
corpus = 2, item = P, topic_id = [(4, 1.0000001)]
corpus = 3, item = L, topic_id = [(6, 1.0)]
corpus = 3, item = O, topic_id = [(6, 1.0)]
corpus = 3, item = W, topic_id = [(6, 0.99999994)]
・・・
corpus = 7, item = C, topic_id = [(0, 0.77635038), (4, 0.22364961)]
corpus = 7, item = T, topic_id = [(0, 0.72590601), (4, 0.27409402)]
corpus = 7, item = Y, topic_id = [(0, 0.1830055), (4, 0.81699443)]
corpus = 7, item = W, topic_id = [(0, 0.1830055), (4, 0.81699443)]
corpus = 7, item = B, topic_id = [(0, 0.14557858), (4, 0.85442138)]
corpus = 7, item = D, topic_id = [(0, 0.1830055), (4, 0.81699443)]
corpus = 7, item = F, topic_id = [(0, 0.74502456), (4, 0.25497544)]
・・・

(4) 可視化

pyLDAvis を使うと LdaModel のトピック内容を可視化できます。

pyLDAvis

pyLDAvis を使うには予め pip 等でインストールしておきます。

インストール例

> pip install pyldavis

可視化1（PCoA）

以下のような処理で Jupyter Notebook 上に D3.js で可視化した結果を表示できます。

トピックの番号は 1 から始まり、デフォルトではソートされてしまう点に注意。

トピックをソートさせたくない（LdaModel 内と同じ順序にしたい）場合は sort_topics = False を指定します。

import pyLDAvis.gensim

vis = pyLDAvis.gensim.prepare(lda, corpus, dic, n_jobs = 1, sort_topics = False)

pyLDAvis.display(vis)

f:id:fits:20180313204240p:plain

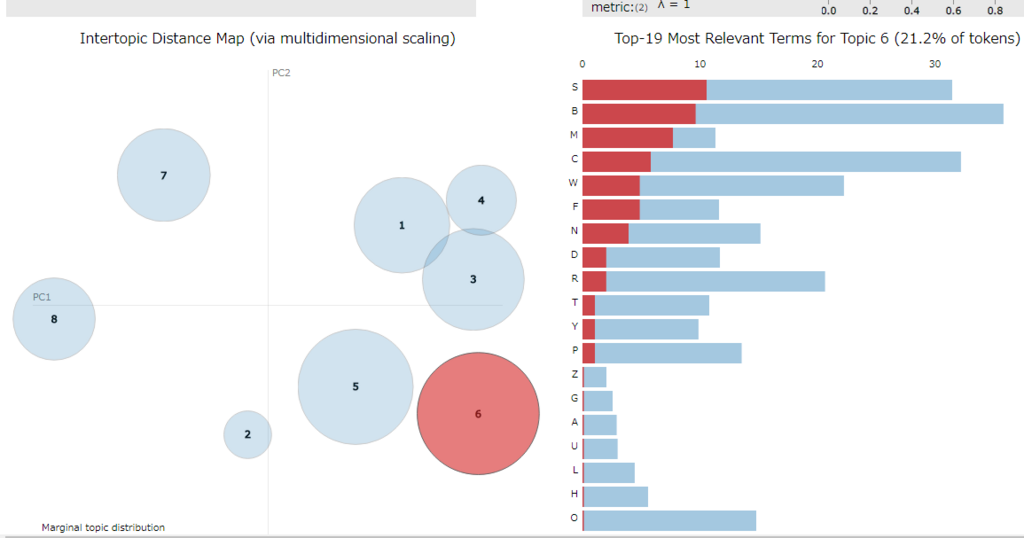
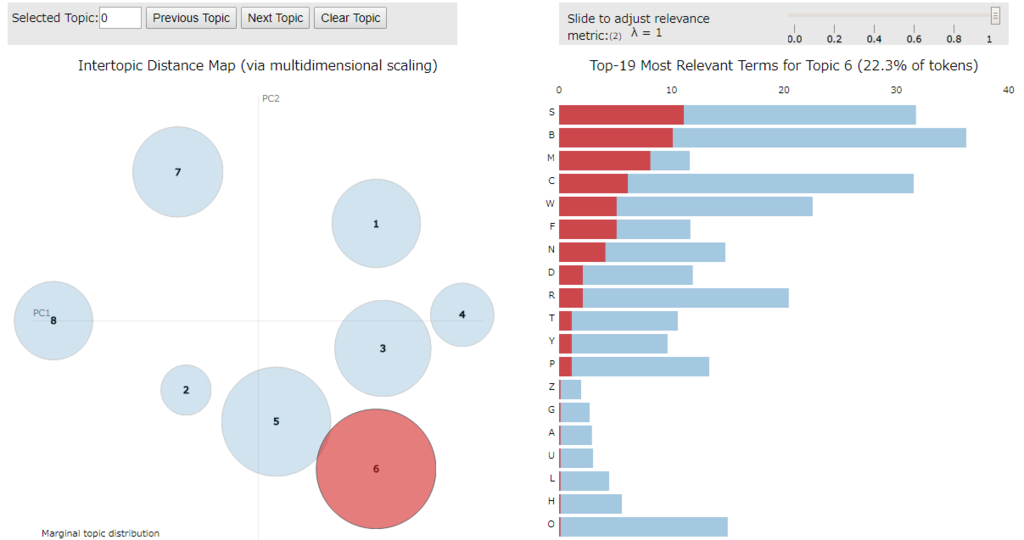
可視化2（Metric MDS）

次元削減の方法としてデフォルトでは PCoA（主座標分析）を使うようですが、mds パラメータで変更できます。

以下は mmds を指定し Metric MDS（多次元尺度構成法）にしてみました。

import pyLDAvis.gensim

vis = pyLDAvis.gensim.prepare(lda, corpus, dic, n_jobs = 1, mds='mmds', sort_topics = False)

pyLDAvis.display(vis)

f:id:fits:20180313204340p:plain

HTML ファイル化

pyLDAvis の結果を HTML ファイルへ保存したい場合は以下のようにします。

import pyLDAvis.gensim

vis = pyLDAvis.gensim.prepare(lda, corpus, dic, n_jobs = 1, sort_topics = False)

pyLDAvis.save_html(vis, 'sample.html')

3. LDA の結果

(a) 併売の組み合わせとトピックの内容

出現数の多い順に（2つの）組み合わせが該当するトピックを抽出してみます。

from itertools import combinations
from toolz import unique

cmb = frequencies([c for s in sentences for c in combinations(sorted(unique(s)), 2)])

for (k1, k2), v in sorted(cmb.items(), key = lambda x: -x[1]):
    topics = lda[dic.doc2bow([k1, k2])]
    print(f"item1 = {k1}, item2 = {k2}, freq = {v}, topics = {topics}")

結果は以下の通りです。

B と S の組み合わせは トピック 5、C と S の組み合わせは トピック 2 で最も確率の高い組み合わせになっていますし、その他も概ねトピック内の確率が高めになっているように見えます。

実行結果

item1 = B, item2 = S, freq = 16, topics = [(5, 0.9663462)]
item1 = C, item2 = S, freq = 14, topics = [(2, 0.9663462)]
item1 = R, item2 = S, freq = 13, topics = [(3, 0.9663462)]
item1 = B, item2 = C, freq = 12, topics = [(5, 0.9663462)]
item1 = B, item2 = W, freq = 12, topics = [(7, 0.9663462)]
item1 = C, item2 = R, freq = 10, topics = [(2, 0.9663462)]
item1 = O, item2 = W, freq = 10, topics = [(7, 0.9663462)]
item1 = C, item2 = N, freq = 10, topics = [(0, 0.9663462)]
item1 = S, item2 = W, freq = 10, topics = [(5, 0.9663462)]
item1 = C, item2 = W, freq = 9, topics = [(7, 0.9663462)]
item1 = B, item2 = R, freq = 9, topics = [(4, 0.9663462)]
item1 = C, item2 = T, freq = 8, topics = [(0, 0.9663462)]
item1 = C, item2 = D, freq = 8, topics = [(2, 0.9663462)]
item1 = C, item2 = F, freq = 8, topics = [(0, 0.9663462)]
item1 = R, item2 = W, freq = 8, topics = [(4, 0.9663462)]
item1 = O, item2 = R, freq = 7, topics = [(6, 0.9663462)]
item1 = B, item2 = D, freq = 7, topics = [(1, 0.9663462)]
item1 = B, item2 = P, freq = 7, topics = [(4, 0.9663462)]
item1 = B, item2 = M, freq = 7, topics = [(5, 0.9663462)]
item1 = C, item2 = Y, freq = 6, topics = [(3, 0.9663462)]
item1 = C, item2 = P, freq = 6, topics = [(0, 0.9663462)]
item1 = B, item2 = O, freq = 6, topics = [(7, 0.9663462)]
item1 = B, item2 = F, freq = 6, topics = [(5, 0.9663462)]
item1 = B, item2 = Y, freq = 6, topics = [(4, 0.9663462)]
item1 = D, item2 = W, freq = 6, topics = [(1, 0.9663462)]
item1 = B, item2 = N, freq = 6, topics = [(5, 0.9663462)]
item1 = N, item2 = S, freq = 6, topics = [(3, 0.9663462)]
item1 = P, item2 = S, freq = 6, topics = [(2, 0.9663462)]
item1 = D, item2 = S, freq = 6, topics = [(1, 0.9663462)]
・・・

(b) アソシエーション分析の結果とトピックの内容

アソシエーション分析で抽出した組み合わせに対するトピックも抽出してみます。

for c in [['B', 'O', 'W'], ['B', 'T', 'C'], ['N', 'C'], ['T', 'C']]:
    topics = lda[dic.doc2bow(c)]
    print(f"items = {c}, topics = {topics}")

こちらもトピックへ概ね反映できているように見えます。

実行結果

items = ['B', 'O', 'W'], topics = [(7, 0.97727275)]
items = ['B', 'T', 'C'], topics = [(0, 0.97727275)]
items = ['N', 'C'], topics = [(3, 0.9663462)]
items = ['T', 'C'], topics = [(0, 0.9663462)]

(c) 未知の組み合わせ

トピックモデルの場合、データセットに無いが潜在的に確率の高そうな組み合わせを抽出する事も可能だと思われます。（有用かどうかは分かりませんが）

例えば、以下のような処理でデータセットに無い組み合わせで確率の高いものから順に 5件抽出してみました。

from toolz import topk

# データセットの組み合わせ
ds = [c for s in sentences for c in combinations(sorted(s), 2)]

topic_terms = lambda i: [(dic[t[0]], t[1]) for t in lda.get_topic_terms(i)]

# トピック毎のデータセットに無い組み合わせ
ts = [
    ((t1[0], t2[0]), t1[1] * t2[1]) 
    for i in range(topic_num) 
    for t1, t2 in combinations(sorted(topic_terms(i), key = lambda x: x[0]), 2)
    if (t1[0], t2[0]) not in ds
]

for (k1, k2), v in topk(5, ts, key = lambda x: x[1]):
    print(f"items1 = {k1}, items2 = {k2}, score = {v}")

実行結果

items1 = C, items2 = G, score = 0.007074854336678982
items1 = G, items2 = R, score = 0.007074854336678982
items1 = G, items2 = S, score = 0.007074854336678982
items1 = O, items2 = Y, score = 0.0069998884573578835
items1 = S, items2 = U, score = 0.00585705041885376

なんとなくな Developer のメモ

トピックモデルを用いた併売の分析 - gensim の LdaModel 使用

1. はじめに

データセット

data.txt

2. LDA の適用

(1) 辞書とコーパスの作成

sentences の内容

dic の内容

corpus の内容

(2) LdaModel 作成

num_topics と alpha

num_topics, alpha と文書あたりの平均トピック数

coherence と perplexity

coherence と perplexity 結果

(3) 結果の出力

show_topics

出力結果

get_topic_terms

出力結果

get_document_topics

出力結果

(4) 可視化

インストール例

可視化1（PCoA）

可視化2（Metric MDS）

HTML ファイル化

3. LDA の結果

(a) 併売の組み合わせとトピックの内容

実行結果

(b) アソシエーション分析の結果とトピックの内容

実行結果

(c) 未知の組み合わせ

実行結果