R で個体差のあるロジスティック回帰2 - MCMCglmm
前回 に続き、今回は個体差を考慮したロジスティック回帰を MCMCglmm で試してみます。
実は MCMCglmm の他にも MCMCpack の MCMChlogit や bayesm の rhierBinLogit 等といろいろ試そうとしてみたのですが、イマイチ使い方が分からなかったので今回は断念しました。
今回使用したサンプルソースは http://github.com/fits/try_samples/tree/master/blog/20140211/
はじめに
今回使用するパッケージを R へインストールしておきます。
install.packages("MCMCglmm")
(2) MCMCglmm を使った階層ベイズモデルによるロジスティック回帰(MCMCglmm 関数)
それでは、前回 と同じデータ (data7.csv) を使って推定と予測線のグラフ化を実施してみます。
MCMCglmm() による推定
MCMCglmm() 関数は glmmML() 関数とほぼ同じ使い方ができますが、
今回のケースでは下記の点が異なります。
- family に multinomial2 を指定する
- デフォルトで個体差 (units に該当) が考慮されるようなので特に id 列を指定する必要はない
デフォルトで詳細(処理状況)が出力されるので、下記では出力しないよう verbose = FALSE としています。
logiMcmcglmm.R
d <- read.csv('data7.csv') library(MCMCglmm) d.res <- MCMCglmm(cbind(y, N - y) ~ x, data = d, family = "multinomial2", verbose = FALSE) summary(d.res) ・・・
実行結果は下記のようになります。
実行結果
> d.res <- MCMCglmm(cbind(y, N - y) ~ x, data = d, family = "multinomial2", verbose = FALSE)
>
> summary(d.res)
Iterations = 3001:12991
Thinning interval = 10
Sample size = 1000
DIC: 667.8652
R-structure: ~units
post.mean l-95% CI u-95% CI eff.samp
units 6.988 3.898 10.58 517.4
Location effects: cbind(y, N - y) ~ x
post.mean l-95% CI u-95% CI eff.samp pMCMC
(Intercept) -4.2271 -6.3586 -2.5264 814.3 <0.001 ***
x 1.0144 0.6117 1.5237 800.3 <0.001 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
各パラメータの平均値 (post.mean) が で、前回の結果(glmmML)と近い値になりました。
ここで units は前回の個体差パラメータ の分散
に該当するようですので、標準偏差とするために平方根を取りました。
プログラム上で上記の結果を使う場合は、MCMCglmm() の結果から
(Intercept, x)の分布を
$Sol で、 (units)の分布を
$VCV で取得できます。
なお、実行する度に若干異なる値になるようなので、何らかのオプションを指定して調整する必要があるのかもしれません。
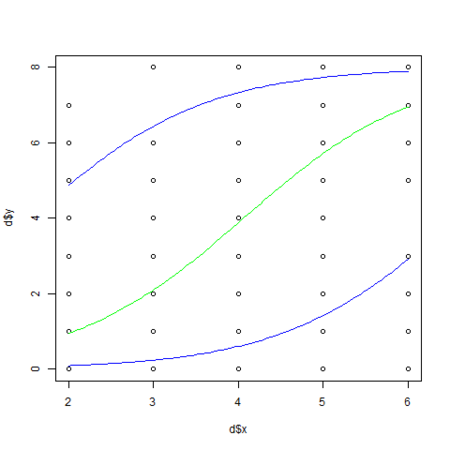
葉数と生存種子数
MCMCglmm() の結果を使って 前回 と同様にグラフ化してみます。
今回はパラメータの平均値(post.mean の値)を使わずに、事後最頻値 (posterior mode) というものを使って予測線を描画してみました。
事後最頻値は posterior.mode() 関数で取得できます。
logiMcmcglmm.R
・・・ # 生存確率の算出 calcProb <- function(x, b, r) 1.0 / (1.0 + exp(-1 * (b[1] + b[2] * x + r))) png("logiMcmcglmm_1.png") plot(d$x, d$y) xx <- seq(min(d$x), max(d$x), length = 100) # beta1 と beta2 の事後最頻値 beta <- posterior.mode(d.res$Sol) # s の事後最頻値 sd <- sqrt(posterior.mode(d.res$VCV)) lines(xx, max(d$N) * calcProb(xx, beta, 0), col="green") lines(xx, max(d$N) * calcProb(xx, beta, -1 * sd), col="blue") lines(xx, max(d$N) * calcProb(xx, beta, sd), col="blue") dev.off() ・・・
ついでに、前々回 のようにpredict() を使って予測線を描画しようとしてみましたが、今のところ predict.MCMCglmm() は新しいデータの指定に対応していないようです。
> predict(d.res, data.frame(x = xx)) Error in predict.MCMCglmm(d.res, data.frame(x = xx)) : sorry newdata not implemented yet
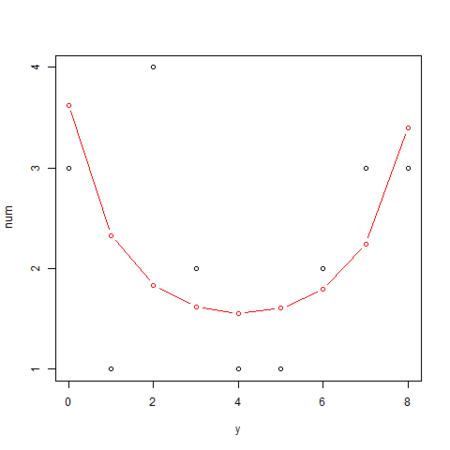
葉数  の種子数分布
の種子数分布
こちらも事後最頻値を使って、前回 と同様にグラフ化してみます。
logiMcmcglmm.R
・・・ png("logiMcmcglmm_2.png") yy <- 0:max(d$N) plot(yy, table(d[d$x == 4,]$y), xlab="y", ylab="num") # 葉数 x を固定した場合の生存種子数 y の確率分布を算出 calcL <- function(ylist, xfix, n, b, s) sapply(ylist, function(y) integrate( f = function(r) dbinom(y, n, calcProb(xfix, b, r)) * dnorm(r, 0, s), lower = s * -10, upper = s * 10 )$value ) lines(yy, calcL(yy, 4, max(d$N), beta, sd) * length(d[d$x == 4,]$y), col="red", type="b") dev.off()