2014-03-02

R でロジスティック回帰とオッズ比の算出 - glm, MCMClogit

R GLM Bayes

以前、glm・MCMCmetrop1R 関数でロジスティック回帰を試みましたが、今回はその時に利用を断念した MCMCpack の MCMClogit 関数を使ってロジスティック回帰を行います。

題材は、書籍「データサイエンティスト養成読本 [ビッグデータ時代のビジネスを支えるデータ分析力が身につく! ] (Software Design plus) 」の p.38 と同様の Titanic データセットを使ったロジスティック回帰とオッズ比の算出です。

以前使ったデータは主に数値でしたが、今回は主に因子（factor）データを扱っている点が異なっています。

今回のソースは http://github.com/fits/try_samples/tree/master/blog/20140302/

はじめに

MCMCpack パッケージを R へインストールしておきます。

install.packages("MCMCpack")

Titanic データセット

Titanic のデータセットは R にデフォルトで用意されており、data.frame(Titanic) すると下記のようになります。

data.frame(Titanic) 結果

> data.frame(Titanic)

   Class    Sex   Age Survived Freq
1    1st   Male Child       No    0
2    2nd   Male Child       No    0
3    3rd   Male Child       No   35
4   Crew   Male Child       No    0
5    1st Female Child       No    0
6    2nd Female Child       No    0
7    3rd Female Child       No   17
8   Crew Female Child       No    0
9    1st   Male Adult       No  118
10   2nd   Male Adult       No  154
11   3rd   Male Adult       No  387
12  Crew   Male Adult       No  670
13   1st Female Adult       No    4
14   2nd Female Adult       No   13
15   3rd Female Adult       No   89
16  Crew Female Adult       No    3
17   1st   Male Child      Yes    5
18   2nd   Male Child      Yes   11
19   3rd   Male Child      Yes   13
20  Crew   Male Child      Yes    0
・・・

内容は以下の通りです。

Class（船室等級）	Sex（性別）	Age（年齢層）	Survived（生存可否）	Freq（人数）
1st, 2nd, 3rd, Crew	Male, Female	Child, Adult	No, Yes	数値

今回は、ロジスティック回帰の結果から船室等級・性別・年齢層毎の生存率に対するオッズ比を算出します。

(1) glm を使ったロジスティック回帰とオッズ比

書籍の内容とほとんど同じですが、まずは glm 関数を使ったロジスティック回帰です。

Survived~. としているので Class・Sex・Age を説明変数としたロジスティック回帰を実施します。

オッズ比は exp(<推定値>) で算出できるので、書籍のような epicalc パッケージは使わず、glm 結果の $coefficients を exp 関数へ渡してオッズ比を算出しました。

logiMcmcglmm.R

d <- data.frame(Titanic)

d.data <- data.frame(
  Class = rep(d$Class, d$Freq),
  Sex = rep(d$Sex, d$Freq),
  Age = rep(d$Age, d$Freq),
  Survived = rep(d$Survived, d$Freq)
)

d.res <- glm(Survived~., data = d.data, family = binomial)
summary(d.res)

# オッズ比
exp(d.res$coefficients)

なお、上記では data.frame(Titanic) の Freq（人数）を展開したデータフレーム（下記）を使ってロジスティック回帰を実施しています。

d.data の内容

   Class    Sex   Age Survived
1    3rd   Male Child       No
2    3rd   Male Child       No
・・・
35   3rd   Male Child       No
36   3rd Female Child       No
・・・

実行結果は下記の通りです。

実行結果

・・・
> d.res <- glm(Survived~., data = d.data, family = binomial)
> summary(d.res)

Call:
glm(formula = Survived ~ ., family = binomial, data = d.data)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.0812  -0.7149  -0.6656   0.6858   2.1278  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   0.6853     0.2730   2.510   0.0121 *  
Class2nd     -1.0181     0.1960  -5.194 2.05e-07 ***
Class3rd     -1.7778     0.1716 -10.362  < 2e-16 ***
ClassCrew    -0.8577     0.1573  -5.451 5.00e-08 ***
SexFemale     2.4201     0.1404  17.236  < 2e-16 ***
AgeAdult     -1.0615     0.2440  -4.350 1.36e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 2769.5  on 2200  degrees of freedom
Residual deviance: 2210.1  on 2195  degrees of freedom
AIC: 2222.1

Number of Fisher Scoring iterations: 4

> 
> # オッズ比
> exp(d.res$coefficients)
(Intercept)    Class2nd    Class3rd   ClassCrew   SexFemale    AgeAdult 
  1.9844057   0.3612825   0.1690159   0.4241466  11.2465380   0.3459219

オッズ比から、女性（Female）は男性（Male）の 11倍（11.2465380）、大人（Adult）は子供（Child）の 3分の1 （0.3459219）の生存率という結果になりました。

(2) MCMClogit を使ったロジスティック回帰とオッズ比

それでは、MCMCpack の MCMClogit 関数を使って同様の処理を実施してみます。

glm 関数の場合とほとんど同じですが、MCMClogit 関数は応答変数（下記の Survived）に因子型（factor）を扱えないようなので、Survived の No と Yes を 0（= No）と 1（= Yes）へ変換しています。（as.numeric(d$Survived) - 1 の箇所）

また、MCMClogit 関数の結果も glm とは違って値の分布となるので summary した結果の平均値（期待値） Mean を使ってオッズ比を算出しています。

logistic_odds_mcmclogit.R

library(MCMCpack)

d <- data.frame(Titanic)

d.data <- data.frame(
  Class = rep(d$Class, d$Freq),
  Sex = rep(d$Sex, d$Freq),
  Age = rep(d$Age, d$Freq),
  Survived = rep(as.numeric(d$Survived) - 1, d$Freq)
)

d.res <- MCMClogit(Survived~., data = d.data)

d.summ <- summary(d.res)

d.summ

#オッズ比
exp(d.summ$statistics[, "Mean"])

実行結果は下記の通りです。

実行結果

・・・
> d.res <- MCMClogit(Survived~., data = d.data)
> 
> d.summ <- summary(d.res)
> 
> d.summ

Iterations = 1001:11000
Thinning interval = 1 
Number of chains = 1 
Sample size per chain = 10000 

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:

               Mean     SD Naive SE Time-series SE
(Intercept)  0.6775 0.2682 0.002682       0.012059
Class2nd    -1.0367 0.1961 0.001961       0.008828
Class3rd    -1.7935 0.1768 0.001768       0.008054
ClassCrew   -0.8607 0.1596 0.001596       0.006971
SexFemale    2.4486 0.1384 0.001384       0.006279
AgeAdult    -1.0540 0.2392 0.002392       0.010882

2. Quantiles for each variable:

               2.5%     25%     50%     75%   97.5%
(Intercept)  0.1455  0.4992  0.6831  0.8630  1.2028
Class2nd    -1.4185 -1.1683 -1.0331 -0.9027 -0.6626
Class3rd    -2.1481 -1.9130 -1.7926 -1.6760 -1.4476
ClassCrew   -1.1764 -0.9661 -0.8651 -0.7535 -0.5488
SexFemale    2.1543  2.3600  2.4525  2.5442  2.7110
AgeAdult    -1.5275 -1.2144 -1.0573 -0.8904 -0.5907

> 
> #オッズ比
> exp(d.summ$statistics[, "Mean"])
(Intercept)    Class2nd    Class3rd   ClassCrew   SexFemale    AgeAdult 
  1.9690188   0.3546137   0.1663746   0.4228566  11.5715841   0.3485381

glm と同じような結果となりました。

最後に、それぞれの値の分布は下記のようになりました。

f:id:fits:20140302174258p:plain

f:id:fits:20140302174314p:plain

2014-02-11

R で個体差のあるロジスティック回帰2 - MCMCglmm

R GLM Bayes

前回に続き、今回は個体差を考慮したロジスティック回帰を MCMCglmm で試してみます。

実は MCMCglmm の他にも MCMCpack の MCMChlogit や bayesm の rhierBinLogit 等といろいろ試そうとしてみたのですが、イマイチ使い方が分からなかったので今回は断念しました。

今回使用したサンプルソースは http://github.com/fits/try_samples/tree/master/blog/20140211/

はじめに

今回使用するパッケージを R へインストールしておきます。

install.packages("MCMCglmm")

(2) MCMCglmm を使った階層ベイズモデルによるロジスティック回帰（MCMCglmm 関数）

それでは、前回と同じデータ（data7.csv）を使って推定と予測線のグラフ化を実施してみます。

MCMCglmm() による推定

MCMCglmm() 関数は glmmML() 関数とほぼ同じ使い方ができますが、今回のケースでは下記の点が異なります。

family に multinomial2 を指定する
デフォルトで個体差（units に該当）が考慮されるようなので特に id 列を指定する必要はない

デフォルトで詳細（処理状況）が出力されるので、下記では出力しないよう verbose = FALSE としています。

logiMcmcglmm.R

d <- read.csv('data7.csv')

library(MCMCglmm)

d.res <- MCMCglmm(cbind(y, N - y) ~ x, data = d, family = "multinomial2", verbose = FALSE)

summary(d.res)
・・・

実行結果は下記のようになります。

実行結果

> d.res <- MCMCglmm(cbind(y, N - y) ~ x, data = d, family = "multinomial2", verbose = FALSE)
> 
> summary(d.res)

 Iterations = 3001:12991
 Thinning interval  = 10
 Sample size  = 1000 

 DIC: 667.8652 

 R-structure:  ~units

      post.mean l-95% CI u-95% CI eff.samp
units     6.988    3.898    10.58    517.4

 Location effects: cbind(y, N - y) ~ x 

            post.mean l-95% CI u-95% CI eff.samp  pMCMC    
(Intercept)   -4.2271  -6.3586  -2.5264    814.3 <0.001 ***
x              1.0144   0.6117   1.5237    800.3 <0.001 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

各パラメータの平均値（post.mean）が ${ \bar \beta_1 = -4.2271, \bar \beta_2 = 1.0144, \bar s = \sqrt{6.988} = 2.643 }$ で、前回の結果（glmmML）と近い値になりました。

ここで units は前回の個体差パラメータ ${ r_i }$ の分散 ${ s ^2 }$ に該当するようですので、標準偏差とするために平方根を取りました。

プログラム上で上記の結果を使う場合は、MCMCglmm() の結果から ${ \beta_1, \beta_2 }$ （Intercept, x）の分布を $Sol で、 ${ s ^2 }$ （units）の分布を $VCV で取得できます。

なお、実行する度に若干異なる値になるようなので、何らかのオプションを指定して調整する必要があるのかもしれません。

葉数と生存種子数

MCMCglmm() の結果を使って前回と同様にグラフ化してみます。

今回はパラメータの平均値（post.mean の値）を使わずに、事後最頻値（posterior mode）というものを使って予測線を描画してみました。

事後最頻値は posterior.mode() 関数で取得できます。

logiMcmcglmm.R

・・・
# 生存確率の算出
calcProb <- function(x, b, r)
    1.0 / (1.0 + exp(-1 * (b[1] + b[2] * x + r)))

png("logiMcmcglmm_1.png")

plot(d$x, d$y)

xx <- seq(min(d$x), max(d$x), length = 100)

# beta1 と beta2 の事後最頻値
beta <- posterior.mode(d.res$Sol)
# s の事後最頻値
sd <- sqrt(posterior.mode(d.res$VCV))

lines(xx, max(d$N) * calcProb(xx, beta, 0), col="green")
lines(xx, max(d$N) * calcProb(xx, beta, -1 * sd), col="blue")
lines(xx, max(d$N) * calcProb(xx, beta, sd), col="blue")

dev.off()
・・・

f:id:fits:20140211122143p:plain

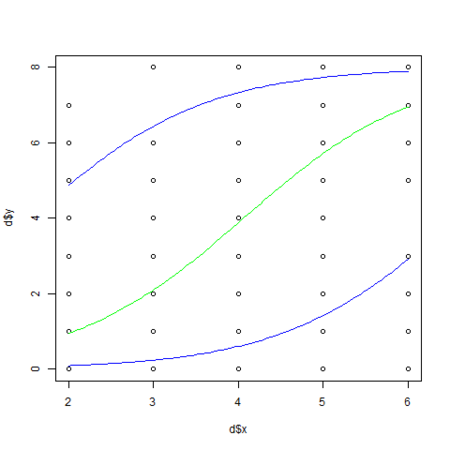
ついでに、前々回のようにpredict() を使って予測線を描画しようとしてみましたが、今のところ predict.MCMCglmm() は新しいデータの指定に対応していないようです。

> predict(d.res, data.frame(x = xx))

Error in predict.MCMCglmm(d.res, data.frame(x = xx)) : 
  sorry newdata not implemented yet

葉数 ${ x_i = 4 }$ の種子数分布

こちらも事後最頻値を使って、前回と同様にグラフ化してみます。

logiMcmcglmm.R

・・・
png("logiMcmcglmm_2.png")

yy <- 0:max(d$N)

plot(yy, table(d[d$x == 4,]$y), xlab="y", ylab="num")

# 葉数 x を固定した場合の生存種子数 y の確率分布を算出
calcL <- function(ylist, xfix, n, b, s)
  sapply(ylist, function(y) integrate(
      f = function(r) dbinom(y, n, calcProb(xfix, b, r)) * dnorm(r, 0, s),
      lower = s * -10,
      upper = s * 10
    )$value
  )

lines(yy, calcL(yy, 4, max(d$N), beta, sd) * length(d[d$x == 4,]$y), col="red", type="b")

dev.off()

f:id:fits:20140211122201p:plain

2014-02-09

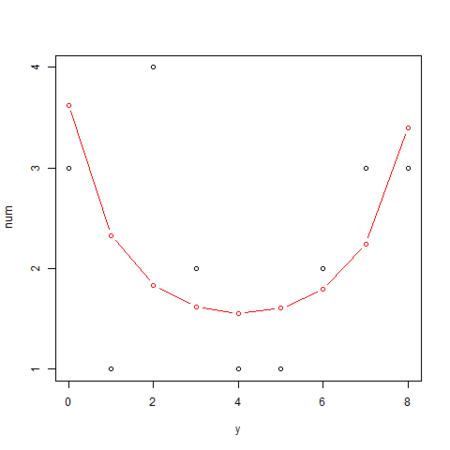
R で個体差のあるロジスティック回帰1 - glmmML

R GLM Bayes

前回のロジスティック回帰に続き、書籍「データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学) 」のサンプルを使って個体差を考慮したロジスティック回帰を GLMM と階層ベイズモデルで試してみます。

(1) GLMM によるロジスティック回帰（glmmML 関数）
(2) MCMCglmm を使った階層ベイズモデルによるロジスティック回帰（MCMCglmm 関数）

ただし、今回は (1) だけで (2) に関しては次回に書く予定です。

サンプルソースは http://github.com/fits/try_samples/tree/master/blog/20140209/

はじめに

パッケージのインストール

今回使用するパッケージを R へインストールしておきます。

install.packages("glmmML")

データ

データは書籍のサポート web サイトから取得します。今回は 7章「一般化線形混合モデル（GLMM）- 個体差のモデリング -」のサンプルデータを使います。

データ data7.csv

"N","y","x","id"
8,0,2,1
8,1,2,2
8,2,2,3
・・・

データ内容は下記の通りです。

項目	内容
N	調査種子数
y	生存種子数
x	植物の葉数
id	個体のID

葉数 ${ x_i }$ の値が 2 ～ 6 までとなっており、葉数毎に 20 個体ずつの生存種子数 ${ y_i }$ をサンプリングしたデータとなっています。（合計 100 個体）

二項分布の性質と過分散

ところで、二項分布の性質として下記があります。
今回のケースでは n が調査種子数（= 8）、p が生存確率です。

(1) 平均（期待値とするのが適切かも）が ${ np }$
(2) 分散が ${ np(1 - p) }$

ここで、今回のデータは下記のようになっています。

葉数 4（x = 4）場合の平均と分散

> mean(d[d$x == 4,]$y)
[1] 4.05

> var(d[d$x == 4,]$y)
[1] 8.365789

np = 4.05 とすると p = 4.05 / 8 = 約 0.5 となり、二項分布として期待される分散は np(1 - p) = 8 × 0.5 × (1 - 0.5) = 2 で、実際の分散 8.36 の方が明らかに大きい値となっています。（過分散）

二項分布として考えると、原因不明な個体差等による効果を考慮した統計モデルを使ったロジスティック回帰が必要となり、GLMM や階層ベイズを使用するという流れとなるようです。

(1) GLMM によるロジスティック回帰（glmmML 関数）

それでは glmmML() 関数を使った推定値の算出とグラフ化を実施してみます。

推定方法

個体差を考慮するため、GLMM では個体差のパラメータ ${ r_i }$ を追加した線形予測子 ${ logit(q_i) = \beta_1 + \beta_2 x_i + r_i }$ を使う事になるようです。
ここで、 ${ q_i }$ は生存確率です。

そして、 ${ r_i }$ が正規分布の確率分布に従っていると仮定し、
確率密度関数 ${ p(r_i | s) = \frac{1}{\sqrt{ 2 \pi s_^2} } \exp(- \frac{r_i ^2}{ 2s ^2 }) }$ を加味して ${ r_i }$ を積分した
尤度 ${ L_i = \int p(y_i | \beta_1, \beta_2, r_i) p(r_i | s) dr_i }$ に対して
全データの積 ${ L(\beta_1, \beta_2, s) = \prod_i L_i }$ の対数尤度 ${ \log L(\beta_1, \beta_2, s) }$ が最大になるようなパラメータ ${ \beta_1, \beta_2, s }$ の最尤推定値を求めます。

なお、 ${ p(y_i | \beta_1, \beta_2, r_i) }$ は二項分布の確率密度関数で、 ${ s }$ は個体差 ${ r_i }$ のばらつき（標準偏差）です。

glmmML() による推定

glmmML() 関数へ指定するオプションは、前回の glm() とほとんど同じですが、下記の点が異なります。

個体差のパラメータ ${ \r_i }$ 部分を cluster オプションで指定

今回は個体毎に異なる値が設定されている id 列を cluster オプションへ指定します。

logiGlmmML.R

d <- read.csv('data7.csv')

library(glmmML)

d.res <- glmmML(cbind(y, N - y) ~ x, data = d, family = binomial, cluster = id)

summary(d.res)
・・・

glmmML() による推定結果は下記の通りです。

実行結果

Call:  glmmML(formula = cbind(y, N - y) ~ x, family = binomial, data = d, cluster = id) 


              coef se(coef)      z Pr(>|z|)
(Intercept) -4.190   0.8777 -4.774 1.81e-06
x            1.005   0.2075  4.843 1.28e-06

Scale parameter in mixing distribution:  2.408 gaussian 
Std. Error:                              0.2202 

        LR p-value for H_0: sigma = 0:  2.136e-55 

Residual deviance: 269.4 on 97 degrees of freedom   AIC: 275.4

${ \hat \beta_1 = -4.190, \hat \beta_2 = 1.005, \hat s = 2.408 }$ と推定されました。

なお、glmmML() の結果から、
${ \hat \beta_1, \hat \beta_2 }$ の値は $coefficients で、 ${ \hat s }$ の値は $sigma で取得できます。

葉数と生存種子数

推定したパラメータを使って葉数 x と生存種子数 y の予測線をグラフ化する処理は下記のようになります。

生存種子数の予測値は 調査種子数（= max(d$N) = 8）× 生存確率 で算出し、
生存確率 ${ q_i }$ は ${ logit(q_i) = \beta_1 + \beta_2 x_i + r_i }$ の式を元に算出します。

logiGlmmML.R

・・・
# 生存確率の算出
calcProb <- function(x, b, r)
    1.0 / (1.0 + exp(-1 * (b[1] + b[2] * x + r)))

png("logiGlmmML_1.png")

# x と y をプロット
plot(d$x, d$y)

# x の範囲（2 ～ 6）を 100分割
xx <- seq(min(d$x), max(d$x), length = 100)

beta <- d.res$coefficients

# 個体差 r = 0 の葉数と生存種子数との予測線
lines(xx, max(d$N) * calcProb(xx, beta, 0), col="green")
# 個体差 r = -2.408 の葉数と生存種子数との予測線
lines(xx, max(d$N) * calcProb(xx, beta, -1 * d.res$sigma), col="blue")
# 個体差 r = 2.408 の葉数と生存種子数との予測線
lines(xx, max(d$N) * calcProb(xx, beta, d.res$sigma), col="blue")

dev.off()
・・・

個体差 r = 0 （個体差なし）とした場合の予測線を緑色で、 r = ±2.408 の予測線を青色で描画しています。

f:id:fits:20140209172056p:plain

葉数 ${ x_i = 4 }$ の生存種子数分布

次に、葉数 x が 4 の場合の生存種子数 y と個体数の分布と予測線をグラフ化する処理は下記のようになります。

glmmML() の結果から、x = 4 の場合の y の確率分布を算出し、x = 4 のサンプル数（= 20）を乗算して予測線を描画しています。

y の確率分布は、0 ～ 8 のそれぞれの値に対して ${ \int p(y_i | \beta_1, \beta_2, r_i) p(r_i | s) dr_i }$ で算出します。（二項分布 × 正規分布を個体差 ${ r_i }$ で積分）

下記では sapply() と integrate() 関数を使って上記の算出処理を実装しています。

なお、lower と upper オプションを使って積分範囲を ${ -10 \times \hat s }$ から ${ 10 \times \hat s }$ としています。

logiGlmmML.R

・・・
png("logiGlmmML_2.png")

# 0 ～ 8
yy <- 0:max(d$N)

# 生存種子数 y と個体数の分布
plot(yy, table(d[d$x == 4,]$y), xlab="y", ylab="num")

# 葉数 x を固定した場合の生存種子数 y の確率分布を算出
calcL <- function(ylist, xfix, n, b, s)
  sapply(ylist, function(y) integrate(
      f = function(r) dbinom(y, n, calcProb(xfix, b, r)) * dnorm(r, 0, s),
      lower = s * -10,
      upper = s * 10
    )$value
  )

# 予測線
lines(yy, calcL(yy, 4, max(d$N), beta, d.res$sigma) * length(d[d$x == 4,]$y), col="red", type="b")

dev.off()

f:id:fits:20140209172110p:plain

今回はここまで。 MCMCglmm を使った階層ベイズは次回。

2013-12-29

R でロジスティック回帰 - glm, MCMCpack

R GLM Bayes

前回に続き、今回も書籍「データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学) 」のサンプルを使って GLM とベイズ統計を試してみます。

題材は、6章「GLM の応用範囲をひろげる -ロジスティック回帰など-」のサンプルデータを使ったロジスティック回帰です。

(1) GLM によるロジスティック回帰（glm 関数）
(2) MCMCpack を使ったベイズ統計によるロジスティック回帰（MCMCmetrop1R 関数）

ここで、MCMCpack のロジスティック回帰に MCMClogit 関数を使えると思ったのですが、使い方がよく分からなかったので MCMCmetrop1R 関数のみ利用しました。

サンプルソースは http://github.com/fits/try_samples/tree/master/blog/20131229/

はじめに

MCMCpack パッケージを install.packages("MCMCpack") で R の実行環境へインストールしておきます。

ロジスティック回帰を試すためのデータは書籍のサポート web サイトから取得できます。

データ data4a.csv

N,y,x,f
8,1,9.76,C
8,6,10.48,C
8,5,10.83,C
・・・

データ内容は下記のようになっており、個体 i それぞれにおいて「 ${ N_i }$ 個の観察種子のうち生きていて発芽能力があるものは ${ y_i }$ 個、死んだ種子は ${ N_i - y_i }$ 個」となっています。

項目	内容
N	観察種子数
y	生存種子数
x	植物の体サイズ
f	施肥処理（C: 肥料なし, T: 肥料あり）

体サイズ x と肥料による施肥処理 f が種子の生存する確率（ある個体 i から得られた 1個の種子が生存している確率）にどのように影響しているかをロジスティック回帰で解析します。

(1) GLM によるロジスティック回帰（glm 関数）

まず、glm 関数を使ったロジスティック回帰を行って予測値の曲線を描画します。

特徴は以下のようになります。

family に binomial （二項分布）を指定（デフォルトのリンク関数が logit となる）
family が binomial で応答変数（cbind(y, N - y) の箇所）が 2値（0, 1）以外なら cbind する必要あり（2値なら y だけでよい）

下記では、生存する確率 ${ q_i }$ の関数が ${ q_i = \frac{1}{1 + \exp(-z_i)} }$ 、
線形予測子 ${ z_i = \beta_1 + \beta_2 x_i + \beta_3 f_i }$ で解析する事になります。

logisticGlm.R

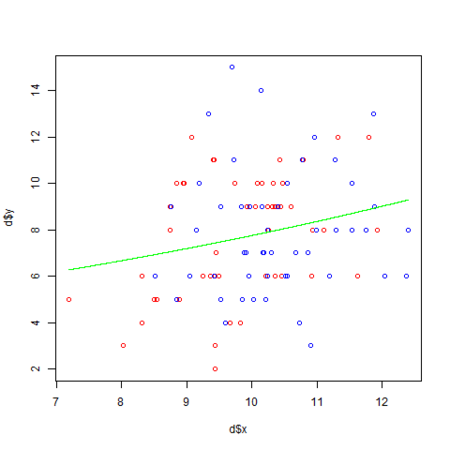
d <- read.csv('data4a.csv')

d.res <- glm(cbind(y, N - y) ~ x + f, data = d, family = binomial)

summary(d.res)

png("logisticGlm.png")
# C: 肥料なしを 赤、T: 肥料ありを 青 で描画
plot(d$x, d$y, col = c("red", "blue")[d$f])

xx <- seq(min(d$x), max(d$x), length = 1000)
ft <- factor("T", levels = levels(d$f))
fc <- factor("C", levels = levels(d$f))
# 下記でも可
#ft <- factor("T", levels = c("C", "T"))
#fc <- factor("C", levels = c("C", "T"))

# T: 肥料ありの予測値を算出
qq.t <- predict(d.res, data.frame(x = xx, f = ft), type="response")
# C: 肥料なしの予測値を算出
qq.c <- predict(d.res, data.frame(x = xx, f = fc), type="response")

# T: 肥料ありの予測値の曲線を 緑 で描画
lines(xx, max(d$N) * qq.t, col = "green")
# C: 肥料なしの予測値の曲線を 黄 で描画
lines(xx, max(d$N) * qq.c, col = "yellow")

dev.off()

predict 関数を使えば glm 結果の回帰モデルから新しいデータによる予測値を求めることができますので、"T:肥料あり" と "C:肥料なし" のそれぞれの予測値を求めて曲線を描画しています。

predict の結果は、生存する確率 ${ q_i }$ の予測値ですので、縦軸が生存種子数 ${ y_i }$ のグラフへ描画するには観察種子数 N （ここでは 8）を乗算する事になります。

ここで、"T:肥料あり" と "C:肥料なし" は factor 関数を使ってファクタ（因子）として作成しています。 d$f と同じ水準を持たせる必要がありますので levels 指定しています。

また、predict には glm で使った説明変数と同じ名前（上記の x と f）を使ったデータを渡す点に注意が必要です。

実行

実行すると下記のような結果になりました。

> R CMD BATCH logisticGlm.R

実行結果 logisticGlm.Rout

・・・
> d.res <- glm(cbind(y, N - y) ~ x + f, data = d, family = binomial)
> 
> summary(d.res)

Call:
glm(formula = cbind(y, N - y) ~ x + f, family = binomial, data = d)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.2584  -0.7948   0.1753   0.8757   3.1589  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -19.5361     1.4138  -13.82   <2e-16 ***
x             1.9524     0.1389   14.06   <2e-16 ***
fT            2.0215     0.2313    8.74   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 499.23  on 99  degrees of freedom
Residual deviance: 123.03  on 97  degrees of freedom
AIC: 272.21

Number of Fisher Scoring iterations: 5
・・・

この結果より、線形予測子 ${ z_i = \beta_1 + \beta_2 x_i + \beta_3 f_i }$ のパラメータ推定値 ${ { \hat\beta_1, \hat\beta_2, \hat\beta_3 } }$ が -19.5361, 1.9524, 2.0215 となります。

f:id:fits:20131229184250p:plain

(2) MCMCpack を使ったベイズ統計によるロジスティック回帰（MCMCmetrop1R 関数）

次は、MCMCpack の MCMCmetrop1R 関数を使ったロジスティック回帰です。

今回のモデルの対数尤度は ${ \log L ( \beta_j ) = \sum_i \log( \small N_i \large C \small y_i \normalsize ) + y_i \log(q_i) + (N_i - y_i) \log(1 - q_i) }$ で、
${ q_i = \frac{1}{1 + \exp(-z_i)} }$ 、
${ z_i = \beta_1 + \beta_2 x_i + \beta_3 f_i }$ なので、
これらを関数化（下記の func）して MCMCmetrop1R 関数へ渡しています。

ちなみに、 ${ \small N_i \large C \small y_i \normalsize = \frac{N_i !}{y_i ! (N_i - y_i) ! } }$ です。（combination）

前回は、項目毎のデータ（d$x や d$y）を func 関数へ渡すようにしていましたが、今回はデータ d を丸ごと渡すようにしました。 MCMCmetrop1R(・・・, data = d, ・・・)

ファクタ（因子）のデータ（d$f）を直接計算に使えないようなので as.numeric で数値化して使っています。

なお、 ${ \log( \small N_i \large C \small y_i \normalsize ) + y_i \log(q_i) + (N_i - y_i) \log(1 - q_i) }$ の部分は dbinom と log 関数を使うとシンプルになります。

パラメータ ${ \beta_1 }$ ${ \beta_2 }$ ${ \beta_3 }$ の初期値は theta.init で c(0, 0, 0) と指定しました。

logisticMcmcMetrop.R

library(MCMCpack)

d <- read.csv('data4a.csv')

func <- function(beta, data) {
  z <- beta[1] + beta[2] * data$x + beta[3] * as.numeric(data$f)
  q <- 1.0 / (1.0 + exp(-z))
  sum(log(choose(data$N, data$y)) + data$y * log(q) + (data$N - data$y) * log(1 - q))

  # 下記でも可
  # sum(log(dbinom(data$y, data$N, q)))
}

d.res <- MCMCmetrop1R(func, theta.init = c(0, 0, 0), data = d, logfun = TRUE)

summary(d.res)

png("logisticMcmcMetrop.png")

plot(d$x, d$y, col = c("red", "blue")[d$f])

xx <- seq(min(d$x), max(d$x), length = 1000)
ft <- factor("T", levels = levels(d$f))
fc <- factor("C", levels = levels(d$f))

zt <- mean(d.res[,1]) + mean(d.res[,2]) * xx + mean(d.res[,3]) * as.numeric(ft)
zc <- mean(d.res[,1]) + mean(d.res[,2]) * xx + mean(d.res[,3]) * as.numeric(fc)

lines(xx, max(d$N) * 1.0 / (1.0 + exp(-zt)), col="green")
lines(xx, max(d$N) * 1.0 / (1.0 + exp(-zc)), col="yellow")

dev.off()

MCMCmetrop1R 結果の各パラメータの mean の値を使って、
肥料の有無（T と C）の生存確率の予測値をそれぞれ算出して、
${ \frac{1}{1 + \exp(-(\hat\beta_1 + \hat\beta_2 x_i + \hat\beta_3 f_i))} }$
観察種子数 N （ここでは 8）を乗算し曲線を描画しています。

実行

実行すると下記のような結果になります。

> R CMD BATCH logisticMcmcMetrop.R

実行結果 logisticMcmcMetrop.Rout

・・・
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
The Metropolis acceptance rate was 0.44590
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
> 
> summary(d.res)

Iterations = 501:20500
Thinning interval = 1 
Number of chains = 1 
Sample size per chain = 20000 

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:

        Mean     SD  Naive SE Time-series SE
[1,] -21.694 1.5583 0.0110185       0.037186
[2,]   1.966 0.1386 0.0009798       0.003322
[3,]   2.027 0.2268 0.0016035       0.005383

2. Quantiles for each variable:

        2.5%     25%     50%     75%   97.5%
var1 -24.836 -22.733 -21.667 -20.596 -18.766
var2   1.703   1.870   1.963   2.059   2.248
var3   1.594   1.873   2.022   2.172   2.494
・・・

Mean の値が glm の結果と似たような値になりました。グラフにすると違いが分からないくらいです。

f:id:fits:20131229184326p:plain

${ \beta_1 }$ の分布

f:id:fits:20131229184348p:plain

${ \beta_2 }$ の分布

f:id:fits:20131229184713p:plain

${ \beta_3 }$ の分布

f:id:fits:20131229184417p:plain

2013-12-15

R でポアソン回帰 - glm, MCMCpack

R GLM Bayes

書籍「データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学) 」の 3章「一般化線形モデル（GLM）」と 9章「GLMのベイズモデル化と事後分布の推定」で説明されていたポアソン回帰を下記のような 3通りで試してみました。

(1) GLM によるポアソン回帰（glm 関数）
(2) MCMCpack を使ったベイズ統計によるポアソン回帰1 （MCMCpoisson 関数）
(3) MCMCpack を使ったベイズ統計によるポアソン回帰2 （MCMCmetrop1R 関数）

書籍では、R から WinBUGS を呼び出して MCMC サンプリングを行っていましたが、今回は R 上でベイズ統計解析を実施する MCMCpack パッケージを試してみました。

サンプルソースは http://github.com/fits/try_samples/tree/master/blog/20131215/

はじめに

まず、MCMCpack パッケージを使用するためにパッケージを R の実行環境へインストールしておきます。

MCMCpack のインストール

> install.packages("MCMCpack")

次に、ポアソン回帰を試すデータを書籍のサポート web サイトから取得してきます。

データ data3a.csv

y,x,f
6,8.31,C
6,9.44,C
6,9.5,C
12,9.07,C
10,10.16,C
・・・

ここで、データの内容は下記のようになっており、体サイズ x と肥料による施肥処理 f が種子数 y にどのように影響しているかをポアソン回帰で解析します。

項目	内容
y	種子数
x	植物の体サイズ
f	施肥処理

(1) GLM によるポアソン回帰（glm 関数）

それでは glm 関数を使ったポアソン回帰を試してみます。ここでは stepAIC() を使った AIC によるモデル選択を試してみました。

poissonGlm.R

d <- read.csv('data3a.csv')

# 説明変数を全て投入したモデル （y ~ x + f と同じ）
d.all <- glm(y ~ ., data = d, family = poisson)

library(MASS)
# AIC によるモデル選択
d.res <- stepAIC(d.all)

summary(d.res)

png("poissonGlm.png")
plot(d$x, d$y, col = c("red", "blue")[d$f])
xx <- seq(min(d$x), max(d$x), length = 1000)
# y ~ x のモデルを使った平均種子数の予測値の曲線を描画
lines(xx, exp(d.res$coefficients["(Intercept)"] + d.res$coefficients["x"] * xx), col="green")
# 以下でも可
#lines(xx, predict(d.res, newdata = data.frame(x = xx), type = "response"), col = "green")
dev.off()

なお、今回は y ~ x のモデルが選択される事（施肥処理は効果が無い）を予め分かっているので、y ~ x のモデルを使って平均種子数の予測値を描画（緑の線）しています。

ここで、 y ~ x モデルのリンク関数（対数リンク関数）は ${ \log \lambda_i = \beta_1 + \beta_2 x_i }$ で、平均種子数 ${ \lambda_i }$ は ${ \lambda_i = \exp (\beta_1 + \beta_2 x_i) }$ となります。

また、 ${ \beta_1 }$ の最尤推定値が d.res$coefficients["(Intercept)"]、 ${ \beta_2 }$ の最尤推定値が d.res$coefficients["x"] に該当します。

実行

実行すると下記のような結果になります。

> R CMD BATCH poissonGlm.R

実行結果 poissonGlm.Rout

・・・
> d.res <- stepAIC(d.all)
Start:  AIC=476.59
y ~ x + f

       Df Deviance    AIC
- f     1   84.993 474.77
<none>      84.808 476.59
- x     1   89.475 479.25

Step:  AIC=474.77
y ~ x

       Df Deviance    AIC
<none>      84.993 474.77
- x     1   89.507 477.29
> 
> summary(d.res)

Call:
glm(formula = y ~ x, family = poisson, data = d)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.3679  -0.7348  -0.1775   0.6987   2.3760  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  1.29172    0.36369   3.552 0.000383 ***
x            0.07566    0.03560   2.125 0.033580 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 89.507  on 99  degrees of freedom
Residual deviance: 84.993  on 98  degrees of freedom
AIC: 474.77

Number of Fisher Scoring iterations: 4

・・・

この結果より、平均種子数の予測値を求める関数は ${ \lambda = \exp(1.29172 + 0.07566 x) }$ になります。

f:id:fits:20131215205033p:plain

(2) MCMCpack を使ったベイズ統計によるポアソン回帰1 （MCMCpoisson 関数）

MCMCpack でポアソン回帰を行うには MCMCpoisson 関数を使うのが簡単だと思います。基本的に glm 関数と同様のモデル式とデータを指定するだけです。

ここでは y ~ x のモデルだけをポアソン回帰してみました。

なお、glm 関数では線形予測子のパラメータ ${ \beta_1 }$ と ${ \beta_2 }$ の最尤推定値を取得しますが、MCMCpoisson 関数では ${ \beta_1 }$ と ${ \beta_2 }$ のそれぞれの分布を取得する点が大きく異なります。

poissonMcmcPoisson.R

library(MCMCpack)

d <- read.csv('data3a.csv')

d.res <- MCMCpoisson(y ~ x, data = d)

summary(d.res)

png("poissonMcmcPoisson.png")
plot(d$x, d$y, col = c("red", "blue")[d$f])
xx <- seq(min(d$x), max(d$x), length = 10000)
lines(xx, exp(mean(d.res[,1]) + mean(d.res[,2]) * xx), col="green")
dev.off()

glm の時とは異なり、 ${ \beta_1 }$ と ${ \beta_2 }$ のそれぞれの算術平均値（mean の結果）を使って、平均種子数の予測値を描画（緑の線）しています。

実行

実行すると下記のような結果になります。

> R CMD BATCH poissonMcmcPoisson.R

実行結果 poissonMcmcPoisson.Rout

・・・
> summary(d.res)

Iterations = 1001:11000
Thinning interval = 1 
Number of chains = 1 
Sample size per chain = 10000 

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:

               Mean     SD Naive SE Time-series SE
(Intercept) 1.29315 0.3602 0.003602       0.010757
x           0.07547 0.0352 0.000352       0.001047

2. Quantiles for each variable:

                2.5%     25%    50%     75%  97.5%
(Intercept) 0.586606 1.05208 1.2956 1.54153 1.9917
x           0.006025 0.05125 0.0756 0.09951 0.1438

・・・

Mean の値が glm の結果とほぼ同じ値になっています。

f:id:fits:20131215205111p:plain

ちなみに、d.res には MCMC サンプリング結果として 1万個の ${ \beta_1 }$ と ${ \beta_2 }$ の値が格納されています。

${ \beta_1 }$ の分布

f:id:fits:20131215205124p:plain

${ \beta_2 }$ の分布

f:id:fits:20131215210052p:plain

(3) MCMCpack を使ったベイズ統計によるポアソン回帰2 （MCMCmetrop1R 関数）

最後に MCMCmetrop1R 関数を使ってみます。

MCMCmetrop1R 関数では自前で定義した尤度関数を使って MCMC サンプリングを実施できるので汎用的に使えます。

今回のモデルの対数尤度は ${ \log L ( \beta_1, \beta_2 ) = \sum_i \log \frac{\lambda_i ^ y_i \exp(- \lambda_i)}{y_i!} }$ で、 ${ \lambda_i = \exp (\beta_1 + \beta_2 x_i) }$ なので、これらを関数化（下記の func）しています。

尤度関数が対数尤度か否かは logfun で指定するようになっており（TRUE の場合が対数尤度）、デフォルト値は TRUE となっています。（今回は対数尤度なので logfun = TRUE です）

また、theta.init で ${ \beta_1 }$ と ${ \beta_2 }$ の初期値を c(0, 0) と指定しています。

poissonMcmcMetrop.R

library(MCMCpack)

d <- read.csv('data3a.csv')

# 尤度関数（対数尤度関数）
func <- function(beta, x, y) {
  lambda <- exp(beta[1] + beta[2] * x)
  sum(log(dpois(y, lambda)))
}

d.res <- MCMCmetrop1R(func, theta.init = c(0, 0), x = d$x, y = d$y, logfun = TRUE)
# 下記でも同じ
#d.res <- MCMCmetrop1R(func, theta.init = c(0, 0), x = d$x, y = d$y)

summary(d.res)

png("poissonMcmcMetrop.png")
plot(d$x, d$y, col = c("red", "blue")[d$f])
xx <- seq(min(d$x), max(d$x), length = 10000)
lines(xx, exp(mean(d.res[,1]) + mean(d.res[,2]) * xx), col="green")
dev.off()

実行

実行すると下記のような結果になります。

> R CMD BATCH poissonMcmcMetrop.R

実行結果 poissonMcmcMetrop.Rout

・・・
> summary(d.res)

Iterations = 501:20500
Thinning interval = 1 
Number of chains = 1 
Sample size per chain = 20000 

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:

        Mean      SD  Naive SE Time-series SE
[1,] 1.29545 0.35797 0.0025313      0.0077477
[2,] 0.07528 0.03498 0.0002473      0.0007561

2. Quantiles for each variable:

         2.5%     25%     50%     75%  97.5%
var1 0.584646 1.05368 1.29884 1.53850 1.9830
var2 0.007798 0.05159 0.07518 0.09907 0.1448

・・・

glm や MCMCpoisson と似たような結果となりました。

f:id:fits:20131215205205p:plain

なお、MCMCpoisson と MCMCmetrop1R ではバーンイン burnin とサンプリング数 mcmc のデフォルト値が異なっています。

関数	burnin のデフォルト値	mcmc のデフォルト値
MCMCpoisson	1000	10000
MCMCmetrop1R	500	20000

はじめに

Titanic データセット

data.frame(Titanic) 結果

(1) glm を使ったロジスティック回帰とオッズ比

logiMcmcglmm.R

d.data の内容

実行結果

(2) MCMClogit を使ったロジスティック回帰とオッズ比

logistic_odds_mcmclogit.R

実行結果

はじめに

(2) MCMCglmm を使った階層ベイズモデルによるロジスティック回帰（MCMCglmm 関数）

MCMCglmm() による推定

logiMcmcglmm.R

実行結果

葉数と生存種子数

logiMcmcglmm.R

葉数 の種子数分布

logiMcmcglmm.R

はじめに

パッケージのインストール

データ

データ data7.csv

二項分布の性質と過分散

葉数 4（x = 4）場合の平均と分散

(1) GLMM によるロジスティック回帰 （glmmML 関数）

推定方法

glmmML() による推定

logiGlmmML.R

実行結果

葉数と生存種子数

logiGlmmML.R

葉数 の生存種子数分布

logiGlmmML.R

はじめに

データ data4a.csv

(1) GLM によるロジスティック回帰 （glm 関数）

logisticGlm.R

実行

実行結果 logisticGlm.Rout

(2) MCMCpack を使ったベイズ統計によるロジスティック回帰（MCMCmetrop1R 関数）

logisticMcmcMetrop.R

実行

実行結果 logisticMcmcMetrop.Rout

の分布

の分布

の分布

はじめに

MCMCpack のインストール

データ data3a.csv

(1) GLM によるポアソン回帰 （glm 関数）

poissonGlm.R

実行

実行結果 poissonGlm.Rout

(2) MCMCpack を使ったベイズ統計によるポアソン回帰1 （MCMCpoisson 関数）

poissonMcmcPoisson.R

実行

実行結果 poissonMcmcPoisson.Rout

の分布

の分布

(3) MCMCpack を使ったベイズ統計によるポアソン回帰2 （MCMCmetrop1R 関数）

poissonMcmcMetrop.R

実行

実行結果 poissonMcmcMetrop.Rout

葉数 ${ x_i = 4 }$ の種子数分布

(1) GLMM によるロジスティック回帰（glmmML 関数）

葉数 ${ x_i = 4 }$ の生存種子数分布

(1) GLM によるロジスティック回帰（glm 関数）

${ \beta_1 }$ の分布

${ \beta_2 }$ の分布

${ \beta_3 }$ の分布

(1) GLM によるポアソン回帰（glm 関数）

${ \beta_1 }$ の分布

${ \beta_2 }$ の分布